ナイーブベイズとは - simplestarの技術ブログ

基本から確かめてみたくなったので
もう一度ナイーブベイズについて確認します。

確率の加法定理と乗法定理の式を使うと、ベイズの定理が導けます。

確率の加法定理とは、ベン図を使うと次のイメージです。
f:id:simplestar_tech:20160424133626j:plain
${ P(A \cup B) = P(A) + P(B) - P(A \cap B)}$

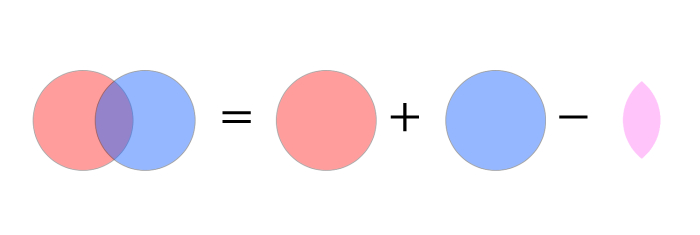
確率の乗法定理とは、ベン図を使うと次のイメージです。
f:id:simplestar_tech:20160424134919j:plain
${ P(A \cap B) = P(A) \times P(B) }$

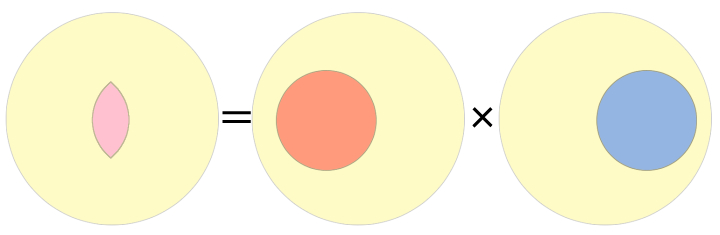
ん？
これだけではベイズの式は導けませんね。

次の条件付き確率のイメージを使います。
f:id:simplestar_tech:20160424141831j:plain
${ P(A \cap B) = P(A|B) \times P(B) }$
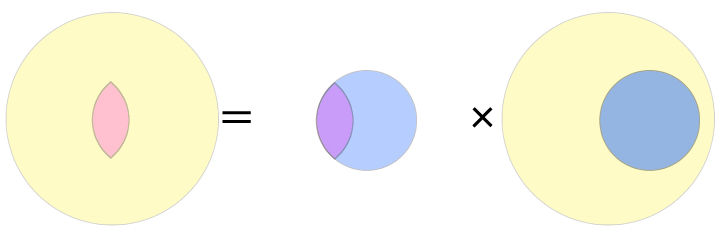
同様に、次のイメージも使って

${ P(A \cap B) = P(B|A) \times P(A) }$

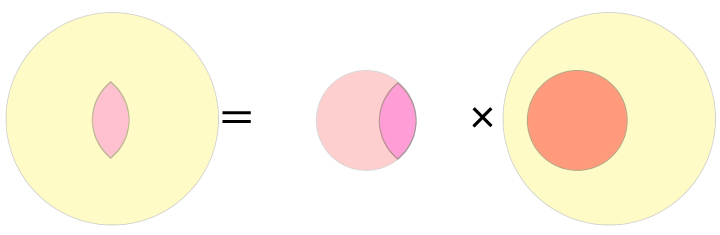
どちらも ${ P(A \cap B)}$ についての式なので

次の等式は組めます。
${ P(A|B) \times P(B) = P(B|A) \times P(A) }$

式を変形すると
${ P(A|B) = \frac{P(B|A) \times P(A)}{P(B)} }$
この式が出ます。
事後確率 ${P(A|B)}$ の計算が、尤度 ${P(B|A)}$ と事前確率 ${P(A)}$ と周辺確率 ${P(B)}$ で行えます。
これがベイズの定理です。

まだ、ナイーブベイズではないので、以降、注意して読んでいってください。

具体的な問題を扱います。

ここで、事象 A を、迷惑メールである、とします。（ ${P(A)}$ は迷惑メールである確率）
事象 B はメールタイトルに「hi」,「% off」が同時に含まれる、とします。（ ${P(B)}$ はメールタイトルに「hi」,「% off」が同時に含まれる確率）

ん？

事象 B は、二つの事象を含んでいますので、事象 B, C と分けないと文章が作れませんね。

するとベイズの式は次の形となります。

${ P(A|B \cap C) = \frac{P(B \cap C|A) \times P(A)}{P(B \cap C)} }$

実際問題を解こうとすると、このベイズの式の尤度 ${P(B \cap C|A)}$ の計算が現実時間で解けなくなります。（組み合わせ爆発により）

そこで、次の考え方を取り入れて問題を単純（ナイーブ）にします。

B, C の事象が本当は互いに独立じゃないのに、独立であるとみなす考え方（単純化、ナイーブにする）を使います。
すると、次の無意味な式が導けます。

${ P(B \cap C|A) = P(B|A) \times P(C|A) }$

この式からは無意味な値しか得られないということを認識してください。
しかし、尤度の計算は極めて高速に終了します。

このような膨大な組み合わせ計算の単純化（ナイーブにする）手法をナイーブベイズと呼びます。

つまり、この問題は
迷惑メールにおけるメールタイトルに「hi」が含まれる確率 ${P(B|A)}$ を集計によって求め
迷惑メールにおけるメールタイトルに「% off」が含まれる確率 ${P(C|A)}$ を集計によって求め
その二つの確率をかけた値に、そもそもの迷惑メールが送られてくる確率 ${P(A)}$ をかけて
メールタイトルに「hi」,「% off」が同時に含まれた時の、迷惑メールである確率 ${P(A|B \cap C)}$ の分子の部分が求まります。

分子の部分？
分母の値が 1 ではない点に注意です。
つまり、次の迷惑メールではない確率も求めなければ、分類問題は解けません。

標準メールにおけるメールタイトルに「hi」が含まれる確率 ${P(B|\bar{A})}$ を集計によって求め
標準メールにおけるメールタイトルに「% off」が含まれる確率 ${P(C|\bar{A})}$ を集計によって求め
その二つの確率をかけた値に、そもそもの標準メールが送られてくる確率 ${P(\bar{A})}$ をかけて
メールタイトルに「hi」,「% off」が同時に含まれた時の、標準メールである確率 ${P(\bar{A}|B \cap C)}$ の分子の部分が求まります。