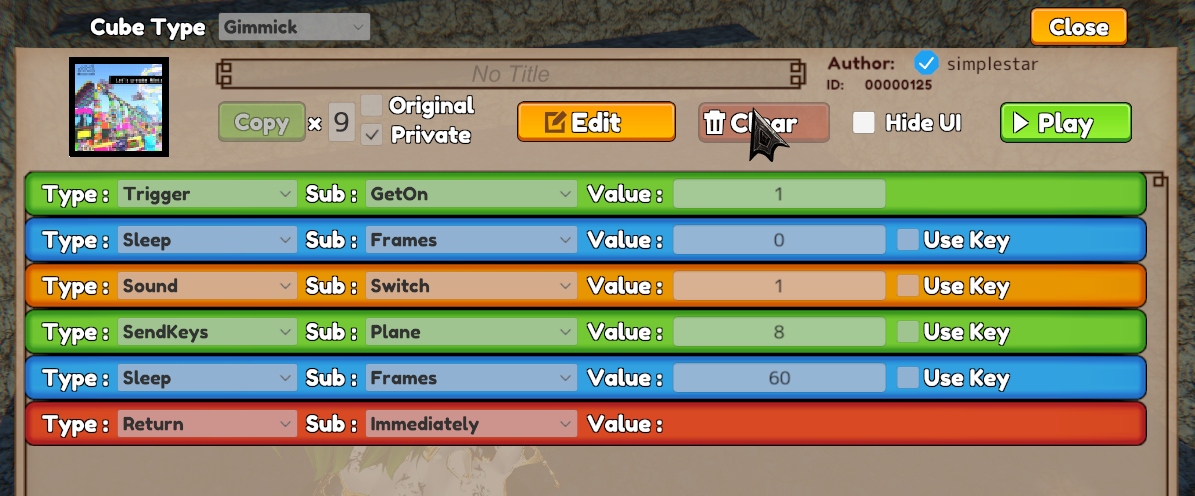
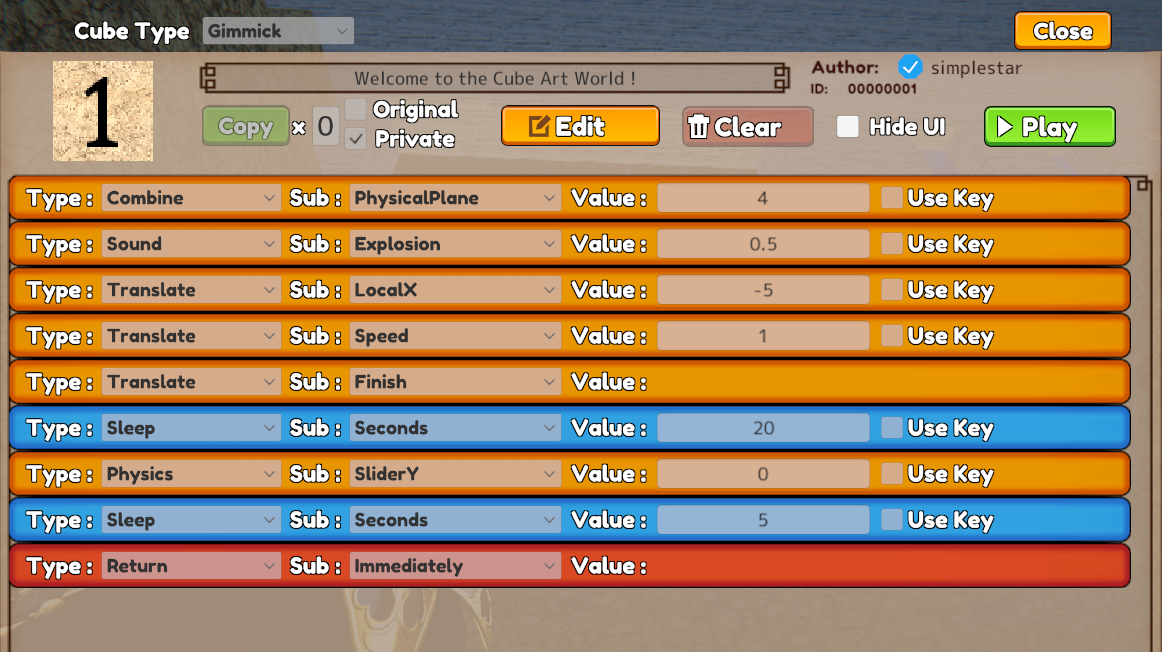
最近 Quest3 を購入しまして、試しに触るVRゲームとして
VRChat はじめたのですが、これがアバター改変とかはじめると楽しくて
今回は自分の勉強がてら、タイトルの通り
手で押すと音が出るオブジェクトを作ってみたいと思います
開発サイクル(初心者用)
VCC と略される CreatorCompanion のインストール
新規プロジェクト作成で Avatars テンプレートを選びます
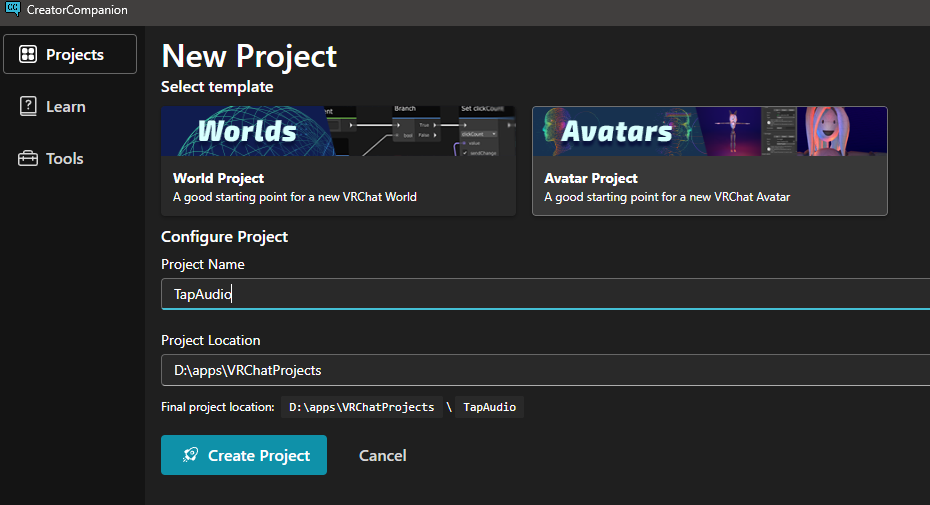
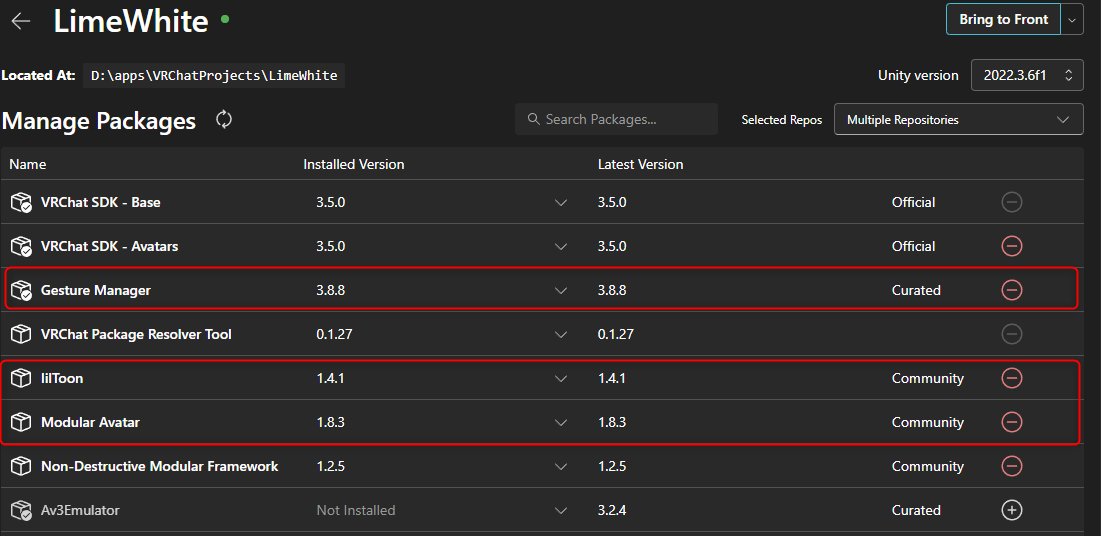
パッケージ管理では
Gesture Manager と Modular Avatar をいれます

Open Project で Unity を開きましょう
Unity バージョンは固定 2019.4.31f1 で開きます
VRChat SDK の Authentication タブで認証しましょう。
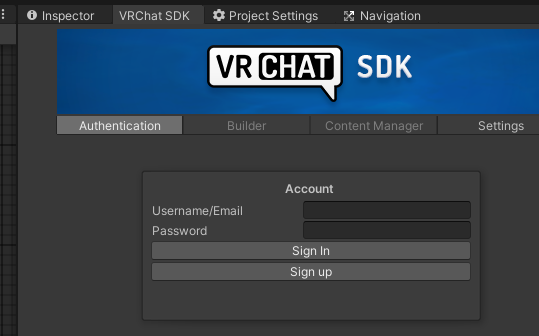
Builder タブで VRChat アバターをテストビルドして試すサイクルを回します
まずは VRC AvatarDescriptor を持つアバターを作りましょう(無いとはじまらない)
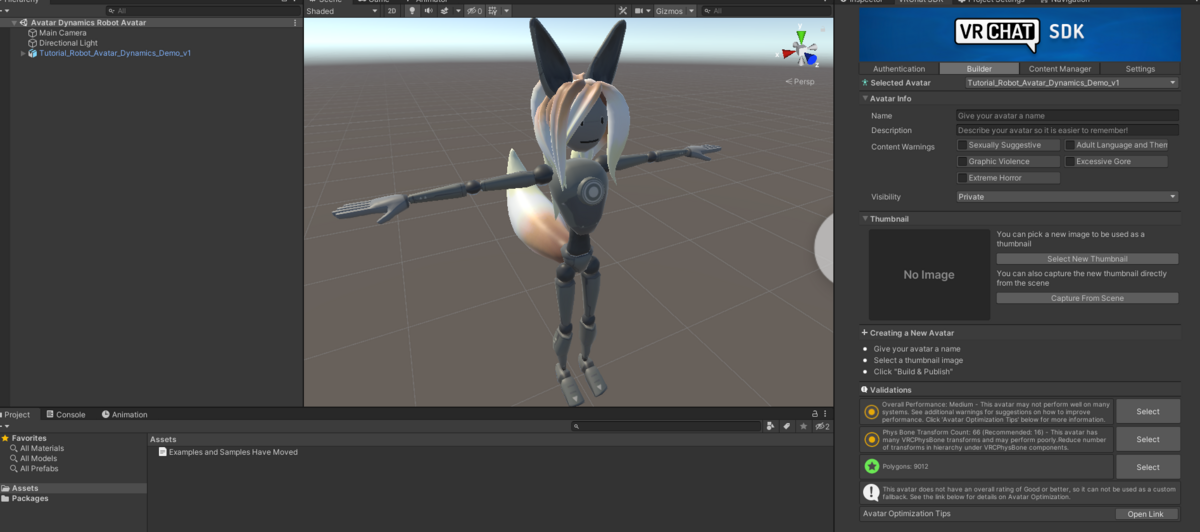
booth とかで気に入ったアバターを買って置くのが良いのですが、今回はサンプルからアバター作ります
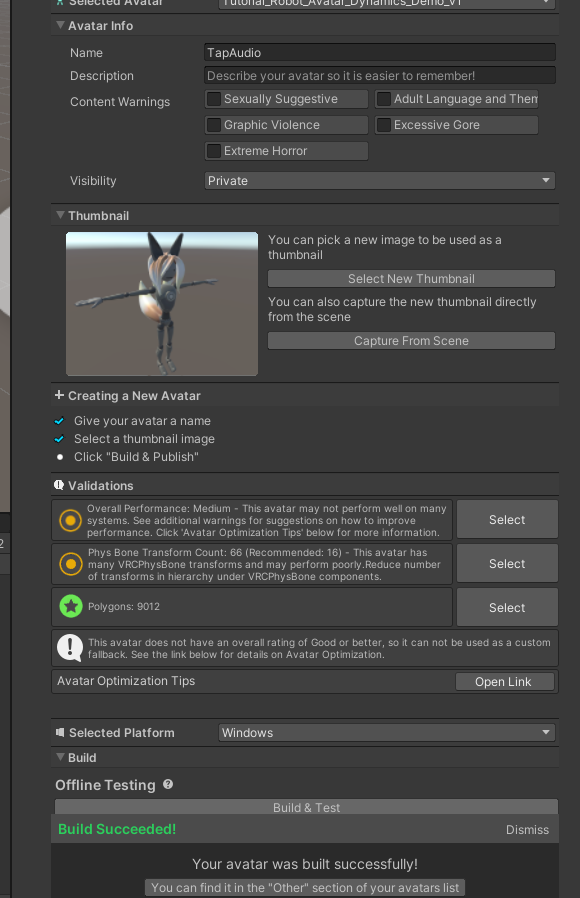
チェックマークにある通り、Name と Thumbnail の画像を登録したら
Build & Test を押して、VRChat にて Other アバターとして選択できるようになります。
Tutorial Robot Avatar の VRC Avata Descriptor の Expressions の Customize ボタンを押します。
VRChat Avatar の ExpressionParameters と ExpressionMenu を作ります

ExpressionMenu の Add Control で申し訳程度に何か項目を足しておきます

割り当てます
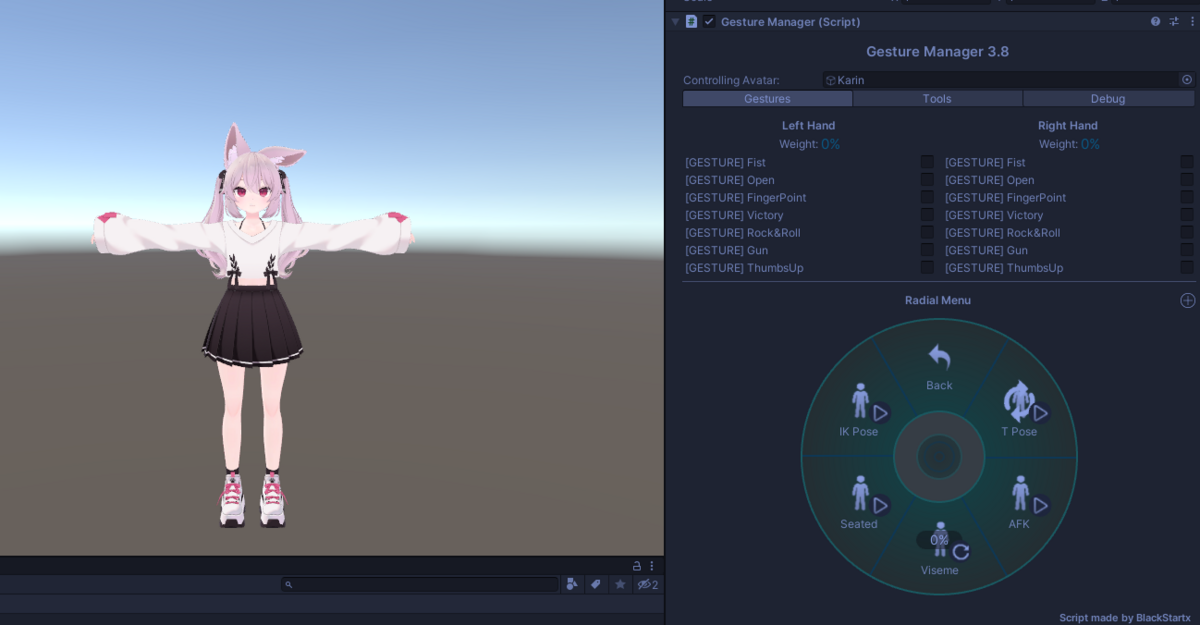
メニューの Tools > Gesture Manager Emulator を選択して、ヒエラルキーに GestureManager オブジェクトを作成
これの Editor ボタン Enter Play-Mode を押します
先ほどの Add Control したメニュー項目が Emulator によって確認できます

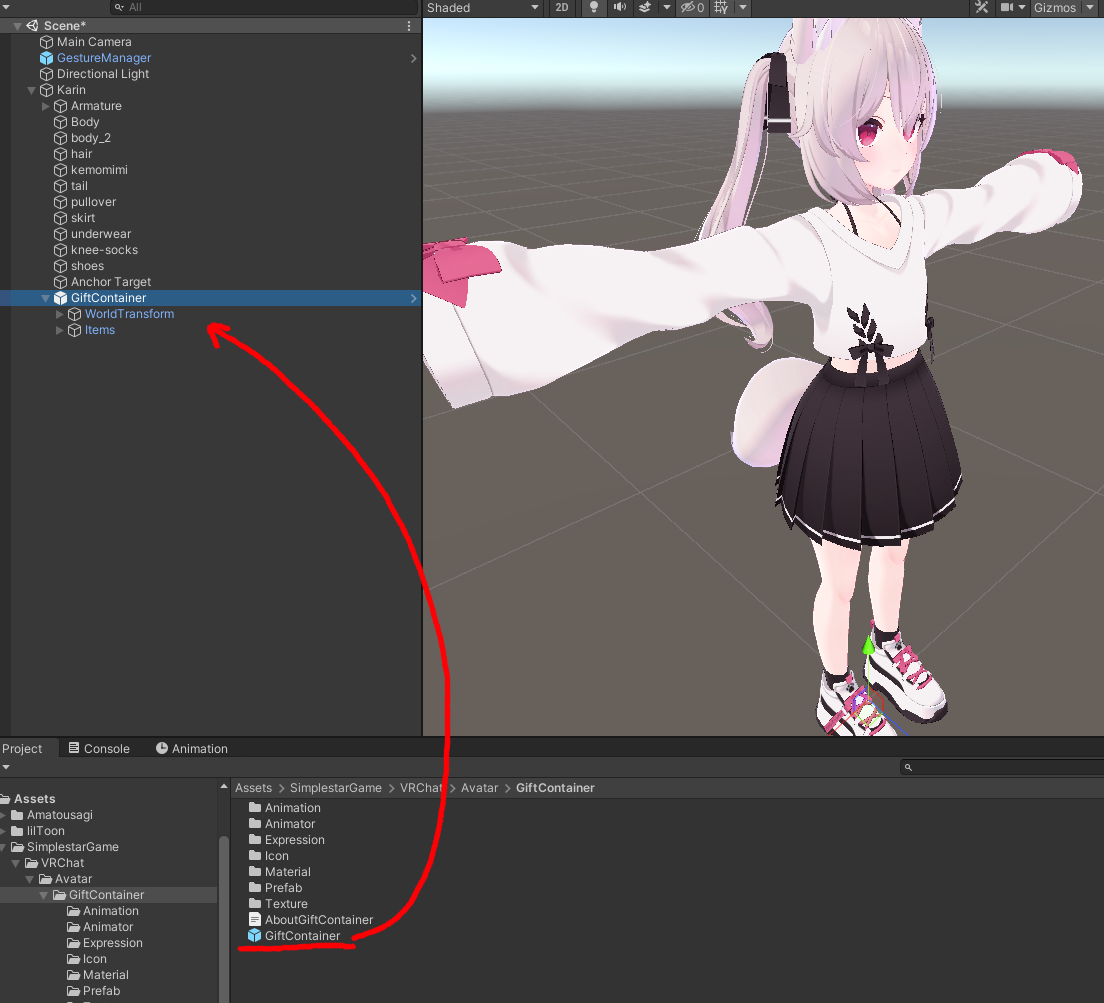
Avatar 直下に空の GameObject を作成して MA Menu Installer を追加します
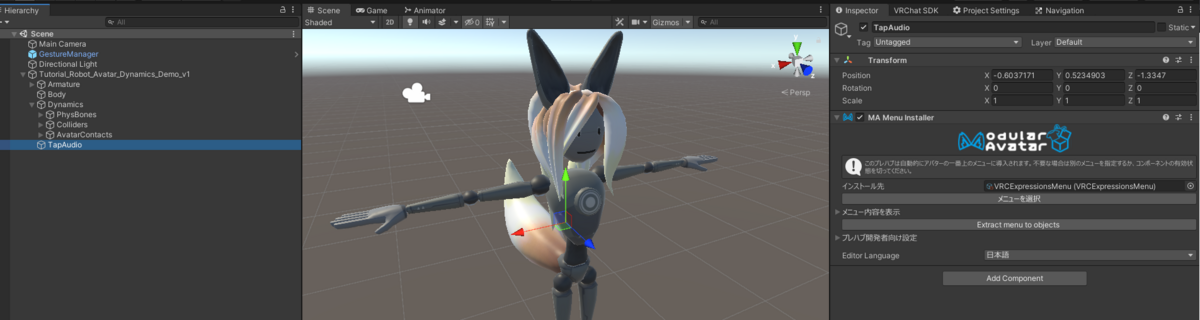
新たに ExpressionMenu を 2つ作り、Main > Sub 関係の設定をします
Main 側のメニュータイプを SubMenu として、Sub 側には Toggle を複数追加します
インストールされるメニューに、Main 側の ExpressionMenu を設定すれば
Gesture Manager の Enter Play-Mode にて
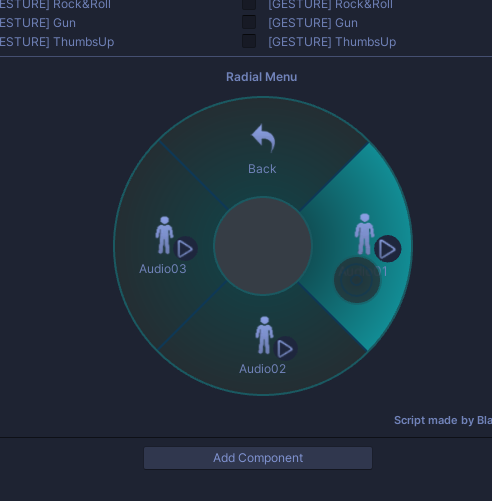
Expression Menu に追加されることが確認できます。
先ほどの MA Menu Installer のオブジェクトに MA Parameters を追加
自動で ExpressionsMenu の Toggle のパラメータが検出されて登録されます
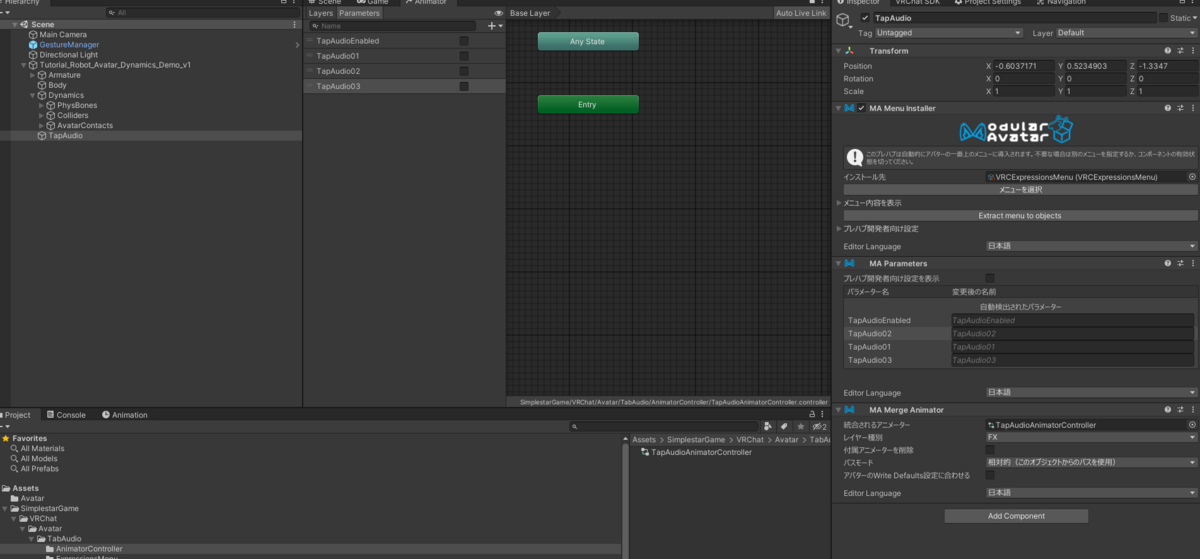
アバターにアタッチされている Animator Controller には手を入れず
ビルド時にMenu と Animator を統合する Modular Avatar (MA)
改変機能の取り外しが容易になる仕組みです
活用していきましょう
オブジェクトの表示・非表示のギミック
MA Menu Installer, MA Parameters をアタッチしているオブジェクトに
MA Merge Animator と Animator Controller を追加し、自動検出された Parameters を
Toggle に見合った Bool 型で Animator Controller に追加します
空の Animation をオン・オフという名前となるように作り
オンオフするオブジェクトごとに Layer 分けしてレイヤーの影響値の Weight を 0 から 1 に設定するのを忘れずに行い
Bool 値の変化で遷移条件を作ります(瞬時に切り替わるように Has Exit Time のチェックを外し Transition Duration は 0 に)
ところで、このHas Exit Time のチェックを外し Transition Duration は 0 にする操作は頻出するので、自動一括設定ツール
Transition Helper を導入すると便利です。
(自分は少し改造して、選択した遷移のみ設定を変更できるようにしました
選択している遷移は次のコードで取得できました
AnimatorStateTransition[] selectedTransitions = Selection.objects.Select(x => x as AnimatorStateTransition).Where(y => y != null).ToArray();
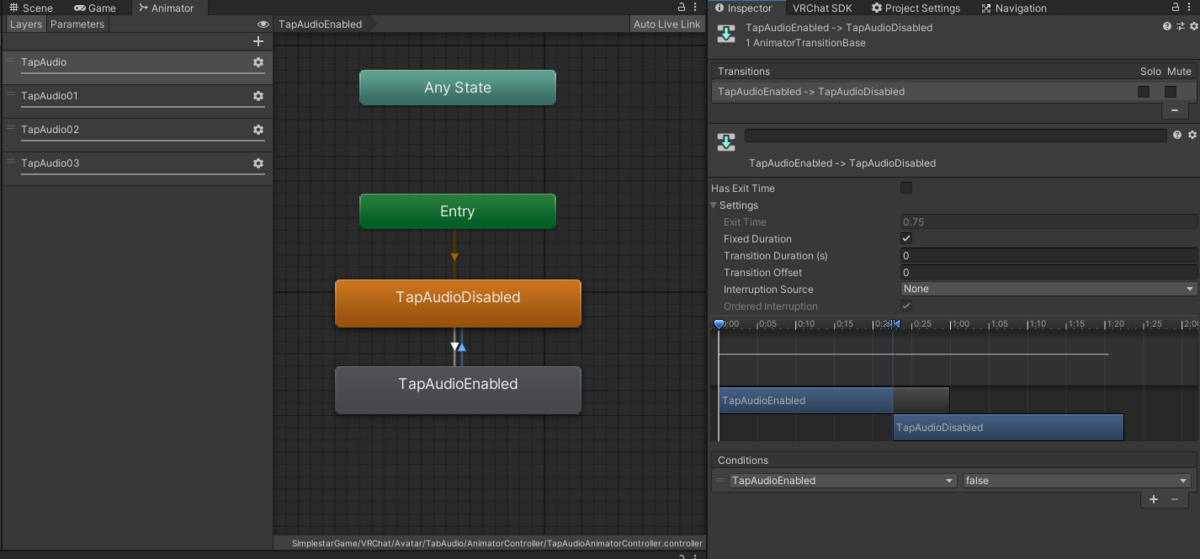
Animation は単純に次のヒエラルキーのオブジェクトの Activate を切り替えるものとします
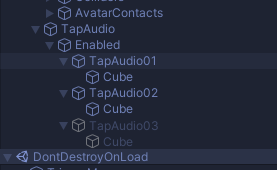
あとは MA Parameters の自動検出パラメータを、Animator のみのタイプから 同期する Bool に変更しておき
これで他プレイヤーとメニュー情報の Bool 値を同期します
ついでに MA Merge Animator の付属アニメーターを削除にチェックを入れておきます
(付属アニメーターは、Animation の録画用に便利なので付けてるだけ)
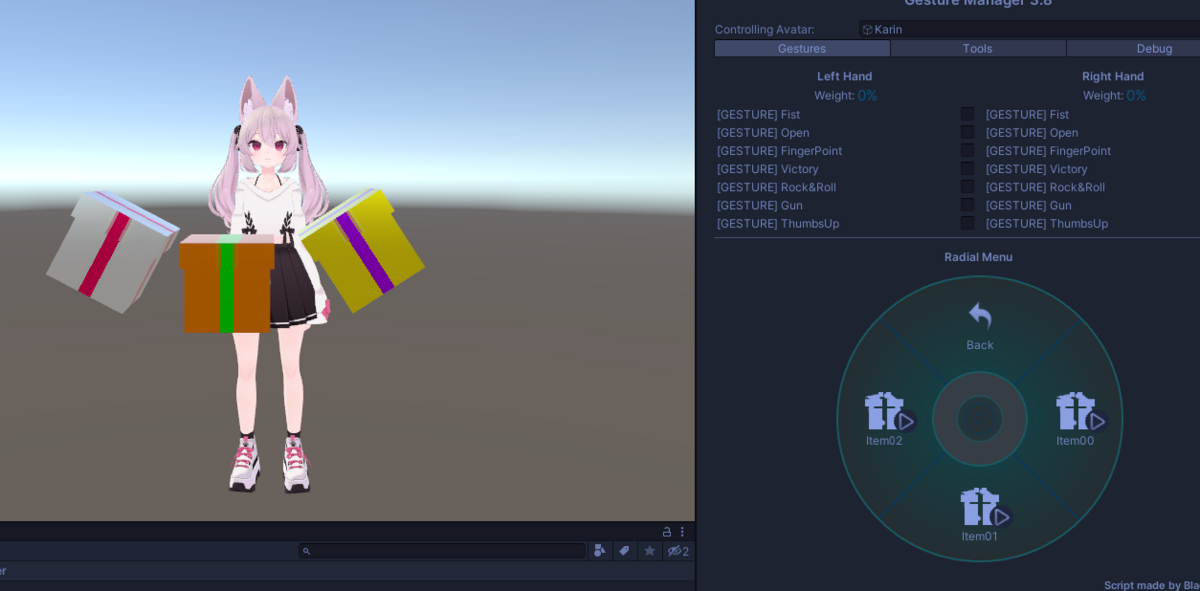
この状態で Gesture Manager の Emulator を起動して Expressions Menu を操作してみると
Emulator の Debug ボタンを押すと、現在の Parameter 一覧と値を確認できます
メニューの Toggle の On Of によって、各オブジェクトが
アクティブ・非アクティブとして切り替わることが確認できます
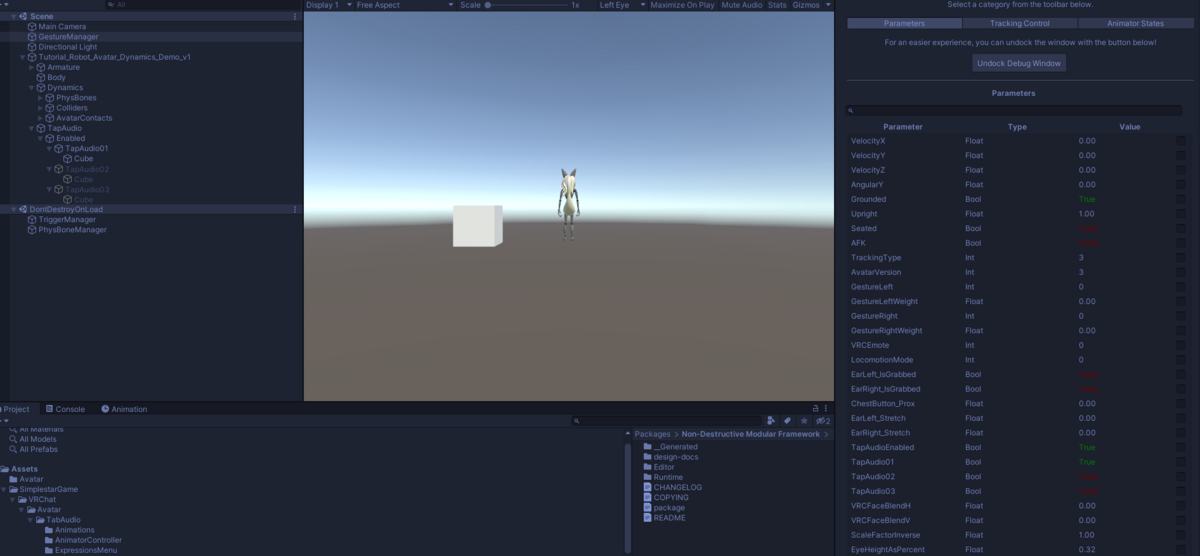
続きは次の記事へ