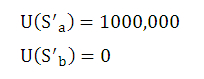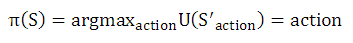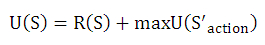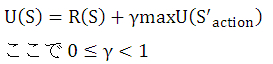強化学習とは?
それは、行動の結果得られる報酬が最も大きくなる行動を選択する仕組みにおいて
その報酬を計算して求めることです。
例えば「働けばお金がもらえる」という場合は「お金」が報酬となります。
報酬の設定のしかたは問題によって、また設定する人それぞれですので、デザイナーとしての腕の見せ所となるでしょう。
今回はお金を報酬にして、強化学習を行う非常に簡単なゲームを作ります。
まず最初に理論的な話を進めます。
お付き合いください。
最初に述べた、行動の結果得られる報酬が最も大きくなる行動を選択する仕組みとは、いったいどういったものなのでしょうか?
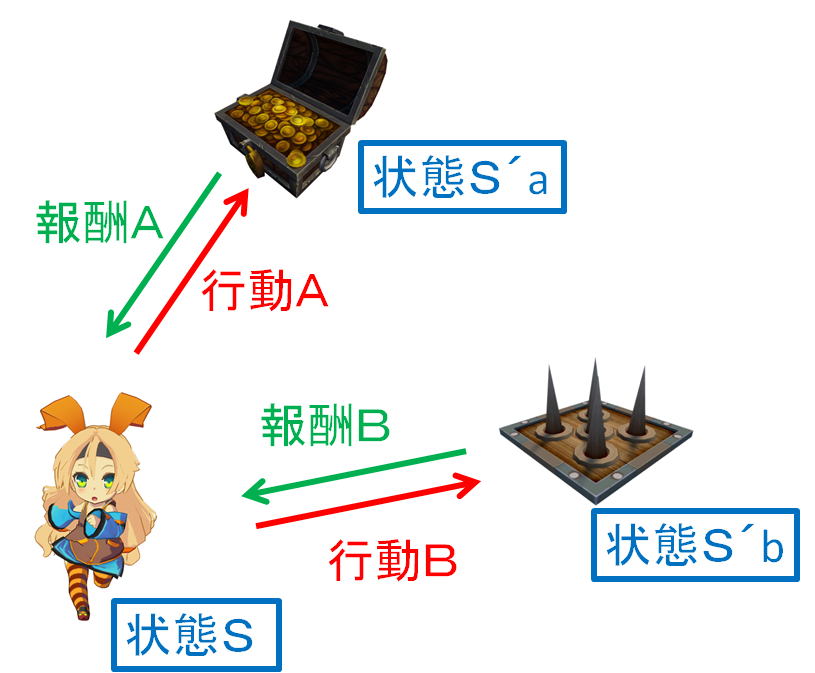
それは、上図の構成において、エージェントと呼ばれるキャラクターが行動Aか行動Bを報酬の大きい方を選んで行動する仕組みのことを指します。
ここで出てくる報酬Aと報酬Bを計算で求めることが強化学習です。
数学の記号を使わず報酬=~という形の計算式を立てると
報酬A=宝箱ゲット、お金いっぱい
報酬B=トラップによるダメージ、ケガしてお金もらえない
と表せます。
次に記号を使って表してみましょう。
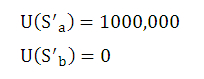
U()で示した値は行動の後、状態S'a, 状態S'b, になったときに得られる金額の値を示しています。
つまり、行動によって得られる報酬です。
この値は今回のデザイナーである私が決めました。(とにかく宝箱側のスコアが高ければ良いという考えで設定しています。)
強化学習で出てくる式で、よく読者の理解を妨げるのが、ここでいう「報酬の大きい値を選択する」という処理まで計算式に含めるところです。
ではその式を見てみましょう。
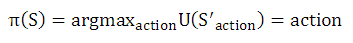
πで表した値は戦略と呼ばれるもので、つまりは行動Aか行動Bいずれかを出力する関数を表します。
argmaxというのは報酬を最大にするactionを選ぶ操作を意味し、つまりは行動Aか行動Bいずれか報酬の大きいactionを選択するということを意味します。
戦略を決めるのは私たち人間です。
今回の私のデザインではactionにaが入ることになるでしょう。
エージェントとなるキャラクター性を示す戦略にすると、きっと愛着のあるAIが作れると思います。
ここまで見てきた計算式について、報酬は人の手によってあらかじめデザインされていますので、代入のみで完結しています。
では、もし報酬がデザインされていない行動が出てきた場合は、どのようにその報酬を設定すればよいのでしょうか?
次の図を見てください。
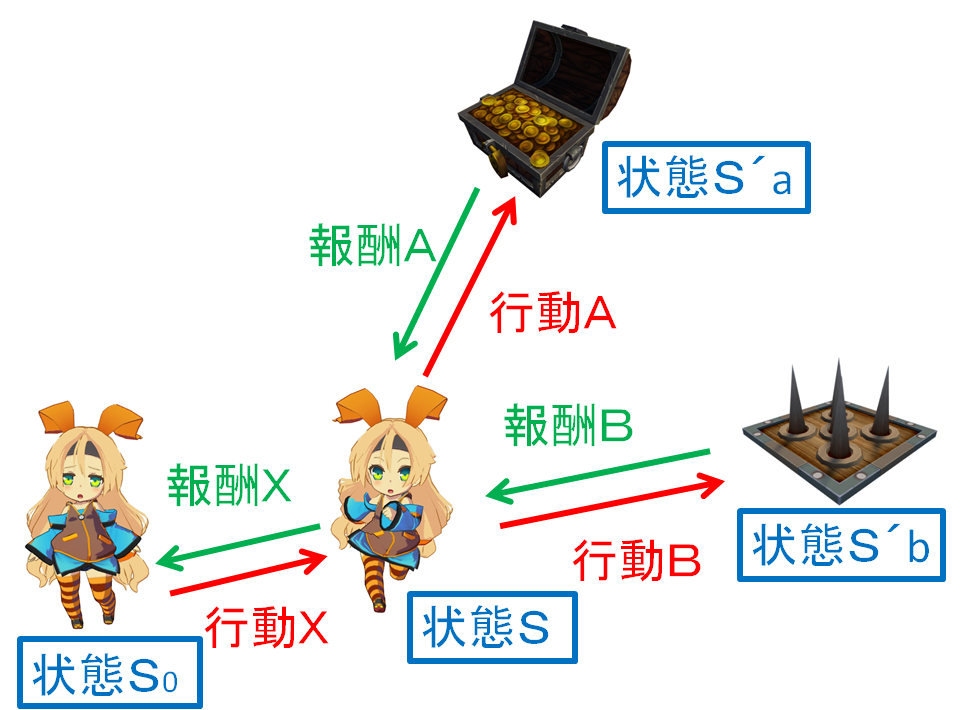
状態Sになる前に、状態S0が存在するとします。
状態S0から状態S0へと進むための行動Xの結果得られる報酬Xはどのようにして求めるか?という問題を今私たちは解こうとしています。
ここで、報酬X=~という数式を立ててみたいと思います。
報酬X=走る、疲れてお金もらえない
確かに、今までの報酬の決め方に従えばこれで完成なのですが、大半の読者は報酬設定が間違っていると指摘できると思います。
そう、状態Sは状態S0に比べてお金持ちになれる可能性が高くなっています。
この期待の高まりを式に反映させたのが次の式です。
報酬X=走る、疲れてお金もらえない + 宝箱ゲット、お金いっぱい or トラップによるダメージ、ケガしてお金もらえない
これが強化学習の説明で最初に出てくる方程式 Bellman equation の原始的な姿です。
そういえば
報酬A=宝箱ゲット、お金いっぱい
報酬B=トラップによるダメージ、ケガしてお金もらえない
と定義していましたので、この原始的な式は次の形で表せます。
報酬X=走る、疲れてお金もらえない + 報酬A or 報酬B
さて、戦略πを採用すると、必ず報酬の大きい方を選ぶことになりますから、今回の私のデザインに従えば、式は次の形になります。
報酬X=走る、疲れてお金もらえない + 報酬A
そろそろ記号を使った数式で報酬Xを表してみます。
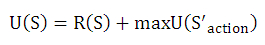
U(S)は状態Sへ進むための行動の報酬Xを表しています。
R(S)は走る、疲れてお金もらえないという状態Sそのものから得られる報酬を表しています。今回の私のデザインであればR(S)=0です。
maxは最も大きな値を選択して返す関数を表しています。
U(S'action)は、報酬Aまたは報酬Bいずれかを示しています。
ここで、報酬Xに報酬Aが減衰することなくそのままの値として代入されてしまいますが、これで本当に良いのでしょうか?
たとえば行動Xを行っている間に、誰かが先に宝箱を開けてお金を持っていってしまっているかもしれません。
そこで、割引率を考慮しようという発想が生まれます。
次の式が広く知れわたっている Bellman equation の姿です。
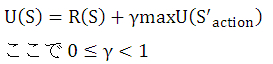
より詳細を学んで、この式が Bellman equation の形と違うと指摘する人が出てくると思いますが
Bellman equation に出てくる Model は、今回の私のデザインでは 1 ですので、確率表記は省略されています。
その方が最初は理解しやすいのでそうしています。
私たちはここまで、「もし報酬がデザインされていない行動が出てきた場合は、どのようにその報酬を設定すればよいのでしょうか?」
という問題に対して考えてきました。
今ならば答えられます。
Bellman equation を使って求めればよいのです。
それでは強化学習を実践してみましょう。
実践編の最初の作業としては、行動の結果得られる報酬が最も大きくなる行動を選択する仕組みというものから作ってみましょう。

作りました。
実装の方も概念を共有した後、コードを示したいと思います。
学習過程にて変動する行動に付随する報酬と、固定された状態に設定される報酬があります。
状態には行動リストがあり、行動には結果の状態があります。
それをつなぎ合わせて、Bellman equation を解く式をプログラムすると次の通り
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public struct StateInfo
{
public float reward;
public ActionInfo[] actions;
}
public struct ActionInfo
{
public float reward;
public StateInfo targetState;
}
public class AgentBehaviour : MonoBehaviour {
public float _gamma = 0.99f;
public StateInfo[] _states = new StateInfo[4];
void Start () {
StateInfo state0 = new StateInfo();
state0.reward = 0;
state0.actions = new ActionInfo[1];
StateInfo state = new StateInfo();
state.reward = 0;
state.actions = new ActionInfo[2];
StateInfo stateA = new StateInfo();
stateA.reward = 1000000;
stateA.actions = null;
StateInfo stateB = new StateInfo();
stateB.reward = 0;
stateB.actions = null;
state0.actions[0].targetState = state;
state.actions[0].targetState = stateA;
state.actions[1].targetState = stateB;
_states[0] = state0;
_states[1] = state;
_states[2] = stateA;
_states[3] = stateB;
int count = 3;
while (0 < --count)
{
Learn();
}
}
private void Learn()
{
for (int i = 0; i < _states.Length; i++)
{
LearnState(ref _states[i]);
}
}
private void LearnState(ref StateInfo state)
{
if (null != state.actions)
{
for (int j = 0; j < state.actions.Length; j++)
{
LearnAction(ref state.actions[j]);
}
}
}
private void LearnAction(ref ActionInfo action)
{
action.reward = action.targetState.reward + _gamma * GetMaxReward(ref action.targetState);
}
private static float GetMaxReward(ref StateInfo targetState)
{
if (null == targetState.actions)
{
return 0;
}
float maxReward = 0;
for (int i = 0; i < targetState.actions.Length; i++)
{
if (maxReward < targetState.actions[i].reward)
{
maxReward = targetState.actions[i].reward;
}
}
return maxReward;
}
}
繰り返し計算を2回すると、行動の報酬が収束することを確認しました。
これが、最も単純な強化学習の例だと思います。
あとは、この学習結果を参照して、最も大きな報酬の行動を選択して行動する仕組みを書けば、ゲームの完成です。
ゲームの実装はハンザツなので省略します。